JBike6

A Benchmark for Bicycle Motion
(linearized ODEs)

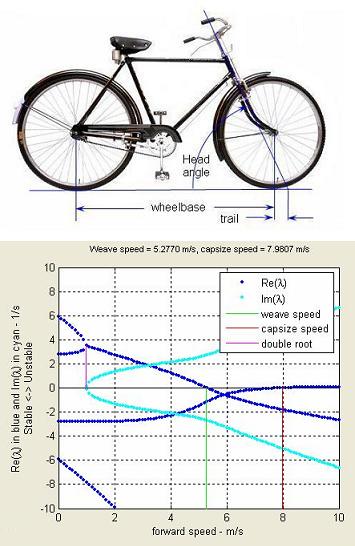
JBike6 is a computer program that determines the stability of bicycles. You can enter information about the shape and mass distribution of a bicycle, and JBike6 calculates the speeds at which that bicycle is stable all by itself, with no control.

In particular, JBike6 calculates the eigenvalues (i.e., perturbation-growth exponents: λ in solutions of the form q = ve^λt), for an idealized, uncontrolled bicycle. It then plots these linearized perturbation-growth eigenvalues over a range of forward speeds. For example, the bike shown at the right is self-stable in the region of speeds (between 5.3 and 8 m/s) where both dark blue lines are below the x-axis.

Before we go any further, however, here are a few caveats you should know:

• This version of JBike6 requires MATLAB by MathWorks.

• If you don't already have MATLAB and wish not to make that investment, you can access much of the functionality with the freeware GNU Octave, but its support for the graphical user interface is limited at best.

• If you'd like to avoid downloading programs at all, you can try an online implementation of JBike6 functionality.

• In any form, JBike6 does not take into consideration many real-world factors, such as:

  • rider inputs to the handlebars,
  • rider motion relative to the bike,
  • flex in the frame, fork, or wheels,
  • any sort of tire behavior,
  • pavement irregularities,
  • aerodynamics,
  • etc.

  Thus, there is no reliable correlation between a bike that looks good according to JBike6, and a bike that riders will like; passive stability of an uncontrolled bicycle has no established correlation with sense of stability in the real world.
  

The equations used in JBike6 are benchmarked exhaustively in a paper by A. L. Schwab, J. P. Meijaard, and J. M. Papadopoulos.

JBike6 has a graphical user interface (screen shot) and comprehensive on-line help.

If working on bicycle or motorcycle development or research, use JBike6 to:

• Calculate no-hands stability of a given design over the entire velocity range. The eigenvalue plot shows exactly at what speed, if any, a configuration becomes stable, and at what speed, if any, it becomes unstable.

• Check the accuracy or validity of any other bicycle or motorcycle equations you may use. JBike6 provides several sets of numbers (benchmarked to high precision) that you can use for comparison.

• Apply control theory. JBike6 provides the necessary linearized equations of motion.

JBike6 was created by:

• Arend L. Schwab, Assistant Professor of Applied Mechanics at Delft University of Technology. Wrote the main JBike6 engine in MATLAB.

• Jim Papadopoulos, Contributing Author of Bicycling Science : Third Edition. Created the JBike concept and monitored its development. Worked closely with Scott Hand on his Master’s Thesis at Cornell University: Comparisons and Stability Analysis of Linearized Equations of Motion for a Basic Bicycle Model

• Andy Ruina, Professor of Theoretical & Applied Mechanics at Cornell University. Lab advisor.

• Andrew Dressel, Graduate Student of Theoretical & Applied Mechanics at Cornell University. Created JBike6 GUI, on-line help, and this JBike6 website.

Download a copy for free. Requires MATLAB, by The MathWorks, version 6.0 or higher.

Please join the Single Track Vehicle Dynamics discussion or email us with questions or comments.

Last updated February 8, 2015