Trampofoil puzzle.
Rules: Prize for first correct response = free cup of coffee or equivalent. Submit solutions to Andy Ruina (ruina@cornell.edu).
Setup: The Trampofoil wing is thin so it is not naturally strong against bending. It holds up its passenger by two struts.
Puzzle: Assuming the pressure distribution on the wing is uniform, where should the struts be placed so that the maximum bending moment along the length is as small as possible.
This is a classic and practicle problem, often called "the bookshelf problem": where to put the two supports under a bookshelf to minimize the maximum bending moment.
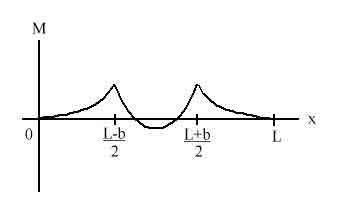
Assume total length L for the wing and distance b between the struts, both equidistant from the center. Each strut exerts a force B. From force balance, the total distributed pressure force equals 2B. Using moment balance to find the bending moment at any point on the wing, we get a graph like the one attached, where the bending moment to the left of the left strut is given by
M = x^2*B/L
and between the struts is
M = x^2*B/L - B(x-L/2+b/2).
To the right of the right strut, it is easily seen that the moments will be
symmetric to the left side.
Thus, the maximum positive moment occurs at the struts and the maximum negative
moment occurs at the centerpoint of the wing.
To make the magnitudes of the opposite extremes as small as possible, set them
equal to each other:
((L-b)/2)^2*B/L = -(L/2)^2*B/L + B(b/2)
which gives:
b = (2 - sqrt(2))L or about .586L.
