Bucket puzzle (Andy Ruina, about 1991).

Rules: Prize for first correct response = free cup of coffee or equivalent. Submit solutions to Andy Ruina (ruina@cornell.edu).

Setup: Prof. Ruina took a tray of water to class and put it on a suspended platform he had built for a demonstration. What he intended was a demo involving putting a finger into the tray. That never happened. What happened was that the tray tipped over and made a big mess of water. Sort of the disaster of the ship Vasa only upside down. Sort of. Your job is to do the calculation he should have done before that lecture demonstration.

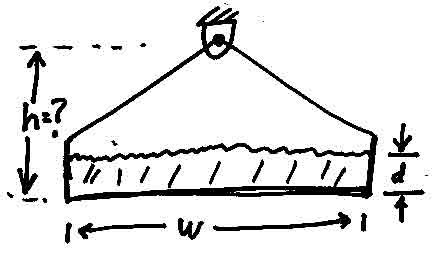
Puzzle: A massless tray with width w is on a massless platform. The tray has water in it with depth d. What is the minimum height h for the suspension point so that the tray is stable? The obvious guess, that h must be at least d/2, is not right (unless the water is frozen).

The walls of the bucket are substantially higher than the water level. So the issue is not about spilling but rather if the bucket is tipped a hair, will it tend to tip more (and then maybe spill).

Answers must be clearly enough explained so the person who reads it can tell it is right without knowing the right answer ahead of time. Solutions must have appropriate sketches. Hard copy solution is fine.

Solution: The answer is that to be stable h must be such that

h   >=     d/2  +  w^2 / (12*d).

Thus, for a w = 18 inch width pan with an inch of water in it we get h>24.5 inches!
In an experiment the weight of the pan will bring this down a little bit, but not much for a light pan.

A non-202 student brousing the www and looking for fun submitted this solution.
A 202 student submitted this solution.

Neither of the above solutions makes clear that the number 12 in the answer is associated with the area moment of
inertia of the surface of the water. We'll give another prize to a solution that makes that evident.